Introduction
Noiz is a simple, configurable, blazingly fast noise library built for and with Bevy.
The primary goal of noiz is to provide high performance implementations of noise algorithms through a very configurable interface. Because noiz is so configurable, it can be difficult to learn compared to other noise libraries. That’s where this book comes in!
By the end of this short book, you will:
- know how to use noiz in your own projects,
- understand how to configure different noise kinds,
- be familiar with what different kinds of noise looks like,
- have an intuition for how noise is implemented,
- get an idea of how to implement custom kinds of noise
If you see anything wrong with this book: unclear explanations, undocumented items, typos, etc, please open an issue on github!
What is noise?
What even is noise? The simple definition is that noise is a kind of randomness in some space. This is best explained with an example:
Imagine you want to generate some trees on a landscape for a video game. Where should the trees go? You could just put them on pre-defined points, maybe a grid of trees with one meter between each tree. But that’s boring, and it doesn’t look very natural. The solution: randomness. For each of those grid points, instead of putting a tree there no matter what, roll some dice, and only place the tree if the dice land a certain way. That’s noise! The dice are a noise algorithm and the way they land are samples of the noise. When you roll the dice (run the algorithm) at different locations, the dice land in different ways (the sample changes). Tada!
In practice, noise is used for much more than just distributing trees/points on a landscape/surface. In scientific computing, it is used to generate data sets. In graphics, it’s used to add variation to an image or scene. In game development, it’s used to introduce an element of “luck”. Most famously, noise is the secret sauce to Minecraft!
Of course, to do all these things, there are a lot of different noise algorithms. Let’s look at that next.
Quick Start
Before using Noiz, remember to also depend on either bevy_math or bevy.
These examples use the more minimal bevy_math.
Randomness
At the heart of every noise algorithm is a random number generator (RNG). We’ll cover how these work in more detail later. For now, all you need to know is that you give the RNG an input, and it gives you back a completely arbitrary number. The random number generator works from a seed you give it. Each number it hands out is based only on the seed it started with and the value you give it.
Here’s an example of a random number generator in Noiz.
use noiz::rng::NoiseRng;
let seed: u32 = 42;
let rng = NoiseRng(seed);
let random_number: u32 = rng.rand_u32(12);Every noise algorithm ultimately comes down to an rng like this.
Noiz does not use the rand crate, instead using its own custom RNG, optimized specifically for noise generation.
Noise Functions
Since every algorithm uses the RNG, noiz has an abstraction, NoiseFunction.
Here’s the short version:
trait NoiseFunction<Input> {
/// The output of the function.
type Output;
/// Evaluates the function at some `input` with this rng.
fn evaluate(&self, input: Input, rng: &mut NoiseRng) -> Self::Output;
}This is an implementation detail, but it will be important later on.
Every noise algorithm in noiz is implemented as a NoiseFunction.
Distribution
A random number generator itself can only generate u32 values, but what if we want something different?
Very commonly, you will want a f32 between 0 and 1 (UNorm) or between -1 and 1 (SNorm).
Here’s how to do that in noiz:
use noiz::{rng::NoiseRng, prelude::*};
let mut rng = NoiseRng(42);
let noise = Random::<UNorm, f32>::default();
let random_unorm = noise.evaluate(12, &mut rng);Random bridges the gap between random u32 values and particular distributions of other types.
The first generic parameter in Random describes the distribution, and the second describes the output type.
In this case, we asked for f32 values between 0 and 1.
But it’s also possible to do other things: Random<SNorm, Vec2> will generate Vec2 values (a 2 dimensional vector) where both x and y are between -1 and 1.
Dividing Space
What if you want to sample a noise function with types other than u32?
In the tree example from earlier, the input might be Vec2 for example.
Due to the nature of random number generation, we can’t just pass in the Vec2.
Instead, we need to divide the vector space (2d, 3d, etc) into different well defined shapes.
Then we can assign a number to each shape and do RNG with that number!
In noiz, those shapes are called DomainCells (since they are a cell of the larger domain),
and the way we cut up the domain is called a Partitioner (since it partitions the domain into cells).
Since noiz integrates with bevy_math, this only works for types that implement the VectorSpace trait, like Vec2.
Here’s how to do this for squares:
use noiz::{rng::NoiseRng, prelude::*};
use bevy_math::prelude::*;
let mut rng = NoiseRng(42);
let noise = PerCell::<OrthoGrid, Random<UNorm, f32>>::default();
let random_unorm = noise.evaluate(Vec2::new(1.5, 2.0), &mut rng);The important part there is PerCell<OrthoGrid, Random<UNorm, f32>>.
This tells noiz that you want values per each cell (DomainCell),
where those cells come from OrthoGrid, a Partitioner that cuts space into unit-length orthogonal chunks (squares, cubes, etc.),
where those values come from the NoiseFunction Random<UNorm, f32>.
There’s a lot of power here: You could change Random<UNorm, f32> to any function you like, and you could change OrthoGrid to any partitioner you like.
For example, PerCell<SimplexGrid, Random<UNorm, f32>>, will make triangles!
More on SimplexGrid later.
Note that the noise function does not need to know the type it is sampled with.
As long as the noise function supports it, you can use anything you like.
For example, we could have used Vec3, Vec4, etc above.
Putting it all together
You might have noticed two small annoyances with this approach:
You keep needing to make NoiseRng values, and there’s no convenient way to scale the noise (make those unit squares bigger or smaller).
To address this, noiz has one more layer of abstraction: Noise.
use noiz::prelude::*;
use bevy_math::prelude::*;
let mut noise = Noise::<PerCell<OrthoGrid, Random<UNorm, f32>>>::default();
noise.set_seed(42);
noise.set_frequency(2.0);
let random_unorm: f32 = noise.sample(Vec2::new(1.5, 2.0));The Noise type just has one generic NoiseFunction and takes care of seeds, rng, and scale.
Each Noise value is deterministic for each seed and can be scaled through either frequency or period.
Note that interacting with
Noisegoes trough various sampling traits, in this caseSampleableFor. Depending on what you want to do with the output, if you want the sample call to be inlined or not, anddyncompatibility, other traits are available.
Note also that not all input types can be scaled. For that (rare) case, there is
RawNoise.
Next, let’s look at some more complex algorithms. As we do, feel free to explore them yourself by running or modifying the “show_noise” example.
cargo run --example show_noise
This example visualizes multiple different kinds of noise algorithms. You can cycle through the different options, change seeds, scales, and vector spaces.
Smooth Noise
Not all noise is smooth. In this chapter, we’ll explore smooth noise in noiz.
White Noise
Let’s remind ourselves of what we made:
use noiz::prelude::*;
use bevy_math::prelude::*;
let noise = Noise::<PerCell<OrthoGrid, Random<UNorm, f32>>>::default();
let value: f32 = noise.sample(Vec2::new(1.5, 2.0));For now, I’ll omit setting the seed and scale of the noise, so we can just focus on the algorithms.
This is white noise, but what does it look like? One of the common ways to get an idea of how a noise algorithm behaves is to visualize it’s results as a color from black to white. Then, make an image using noise samples as the pixel values. That let’s us visualize this noise as:

We could have also used triangular cells via SimplexGrid.
Just like OrthoGrid is built on orthogonal primitives (squares, cubes, etc), SimplexGrid is built on simplex primitives (triangles, tetrahedrons, etc).
Using SimplexGrid instead of OrthoGrid would produce:

But for now, let’s focus on squares.
Anyway, this is white noise, and it’s not usually very useful. There’s no form or flow to it; it’s random, but it’s certainly not very natural or organic looking. Put another way, this noise is rough, but we want smooth noise.
Note that, due to compression, not all details of noise may be clear on these images. And, to prevent a large download size, not all noise combinations will have an image. There’s simply too many combinations of noise settings, which is a good problem to have! Also, the scale of the noise may change between images to better show detail, etc.
Value Noise
If you were tasked with making this rough noise smoother, how would you approach it? One way you might think of is to blur the lines between the squares. That’s values noise!
Basically, instead of picking a value for each domain cell, pick one for each corner of the domain cell, and mix those values together across the cell. If that didn’t make sense, see a visual explanation here, which covers both value and perlin noise; more on perlin in a bit. This is called bilinear interpolation. In noiz, we call this mixing, as it is generalized for squares, cubes, and hyper cubes.
use noiz::prelude::*;
use bevy_math::prelude::*;
let noise = Noise::<MixCellValues<
OrthoGrid,
Linear,
Random<UNorm, f32>,
>>::default();
let value: f32 = noise.sample(Vec2::new(1.5, 2.0));Here, MixCellValues is told to mix values over each domain cell, sourced from OrthoGrid, by the Linear curve, where each value comes from Random<UNorm, f32>.
Note that
MixCellValuesonly really works withOrthoGridvariants (more on those later) or a customPartitioneryou make. It is possible to implement mixing for other shapes, but they are not worth it for the runtime cost.
Regardless, values noise produces this:

But what are all those harsh lines doing in the noise?
Sometimes, that’s what you want; most of the time, you want smoother.
Thankfully, there’s a curve for that.
Changing Linear to Smoothstep, unsurprisingly, makes the image smoother:

This is traditional value noise.
It’s so common, noiz provides a type alias for it in prelude::common_noise.
This generic curve parameter runs on bevy_math’s Curve trait,
so you can also use ones in their library or make you’re own.
Depending on what you want, Smoothstep is almost always the right choice for mixing.
Though, sometimes Linear or a custom curve is artistically appealing.
When picking the curve, keep in mind that the more derivatives that can be taken from a curve, the smoother the result generally appears. For example,
Linearproduces harsh changes in the noise, as you saw. Then,Smoothstepeliminated those abrupt changes, but the derivative of the noise, how the value is changing, still has sharp changes of it’s own! When you care about the smoothness of the derivative of noise, you may want to use a smoother curve. For that, noiz also providesDoubleSmoothstep,Smoothstepcomposed on itself.
Perlin Noise
Maybe you weren’t satisfied with the value noise. Sure, it’s better than white noise, but it’s still pretty recitative. I mean, the values are random and smooth, but the shapes are still easy to spot. It’s just a bunch of blurry squares!
That’s where perlin noise comes in! Instead of mixing random values over a domain cell, source those values partly from the sample location and partly from a random unit vector. That probably won’t make sense at first (and that’s ok). If you want a visual explanation, see here again. Ultimately, since the sample location has more effect, this adds lots more shapes to the noise. Here’s how this works in noiz:
use noiz::prelude::*;
use bevy_math::prelude::*;
let noise = Noise::<MixCellGradients<
OrthoGrid,
Smoothstep,
QuickGradients,
>>::default();
let value: f32 = noise.sample(Vec2::new(1.5, 2.0));Here, MixCellGradients is told to mix those unit vector + sample location combinations over domain cells from OrthoGrid, via the Smoothstep curve.
Those unit vectors are called gradients, and we specify how to make them, here with QuickGradients.
Usually QuickGradients is the right choice; it provides fast, decent gradients.
Any time this “random unit vector combined with sample location” trick is used, it’s called gradient noise, since it comes from, well, gradients. Noise that just merges random values directly is generally called value noise, even if it isn’t the traditional value noise described above.

Isn’t that nice?
This is so common, it has a type alias for it in prelude::common_noise.
Perlin noise isn’t perfect.
If you look closely, you’ll see directional artifacts: places that seem to form lines together.
This isn’t always a big deal, but it can be minimized with other gradient generators that sacrifice speed for quality.
Some of these are also provided in Noiz, with various trade-offs.
See here.
Perlin noise mixes values, just like value noise, so the same restrictions on
Partitioners apply here too. Additionally, the same configuration operations for the curve apply here too:DoubleSmoothstepmay sometimes be needed, andLinearwill produce rougher noise.
Simplex Noise
Even with a high quality gradient generator, perlin noise can and will generate directional artifacts from time to time. Usually, this isn’t a big deal; sometimes, it’s even desirable—but not always. In those cases, simplex noise is the solution.
Instead of being based on squares, it’s based on triangles. This eliminates straight linear artifacts, though some zig-zagy ones may remain. Still, that’s about as good as one can ask for.
One issue with using triangles is that it’s very inefficient to mix values over them. Instead, simplex noise blends values. What’s the difference? Think of it like this: mixing is like a movie blurring to transition between two scenes; blending is like the movie fading to black from one scene before fading from black to a new scene. It’s an imperfect analogy, but hopefully it gives you an idea. If you want the details, check out this paper.
Before jumping into simplex, here’s what blending cell values looks like instead of mixing them:
use noiz::prelude::*;
use bevy_math::prelude::*;
let noise = Noise::<BlendCellValues<
OrthoGrid,
SimplecticBlend,
Random<UNorm, f32>,
>>::default();
let value: f32 = noise.sample(Vec2::new(1.5, 2.0));Here, BlendCellValues is told to blend values from Random<UNorm, f32> between the points of domain cells from OrthoGrid.
Of course, we also must specify how to blend them.
The simplest, and usually the best, blender is SimplecticBlend.
It produces pleasing, round results, but there are other blenders too, which we’ll see later in the book.
This produces:

Wow, we’re back to the same repetitiveness from value noise. But we don’t want value noise, we want gradient noise! Here’s blended gradient noise on a square grid:
use noiz::prelude::*;
use bevy_math::prelude::*;
let noise = Noise::<BlendCellGradients<
OrthoGrid,
SimplecticBlend,
QuickGradients,
>>::default();
let value: f32 = noise.sample(Vec2::new(1.5, 2.0));This produces:

Well, that’s better, but it still has those grid lines!
Now for the last step: using triangles to remove grid lines via SimplexGrid.
Here’s it at work:
use noiz::prelude::*;
use bevy_math::prelude::*;
let noise = Noise::<BlendCellGradients<
SimplexGrid,
SimplecticBlend,
QuickGradients,
>>::default();
let value: f32 = noise.sample(Vec2::new(1.5, 2.0));The above produces:

Tada!
Traditional simplex noise.
This is also so common that it has a type alias in prelude::common_noise.
Simplex noise still isn’t perfect, but it is more than good enough in practice.
It might surprise you, but value, perlin, and simplex noise are not the only ways to smooth out white noise. Let’s look at another…
Distance Noise
Mixing and blending is not the only way to smooth out rough white noise. When thinking about how to smooth it out, another idea you might have had is to pick some point in each cell and generate values based on that point instead of the whole cell. Then, you could return results based on the sample’s location relative to those points instead of just what cell it lands in. This is considered distance noise since it is ultimately always tied to the distance between points.
Cellular Noise
Let’s start simple.
For each sample location, first, find it’s domain cell, then find the nearest corner of that cell, then generate a value based on that corner.
This is called cellular noise because it ends up creating “cells” of values.
These cells are not to be confused with domain cells from a Partitioner; you can think of them as a desirable side affect of the algorithm
Here’s how to do cellular noise in noiz:
use noiz::prelude::*;
use bevy_math::prelude::*;
let noise = Noise::<PerNearestPoint<
SimplexGrid,
EuclideanLength,
Random<UNorm, f32>,
>>::default();
let value: f32 = noise.sample(Vec2::new(1.5, 2.0));Here, PerNearestPoint is told to find the cell of the sample via SimplexGrid,
find the nearest corner of that cell via the distance function EuclideanLength,
and generate a value there via Random<UNorm, f32>.
This produces:
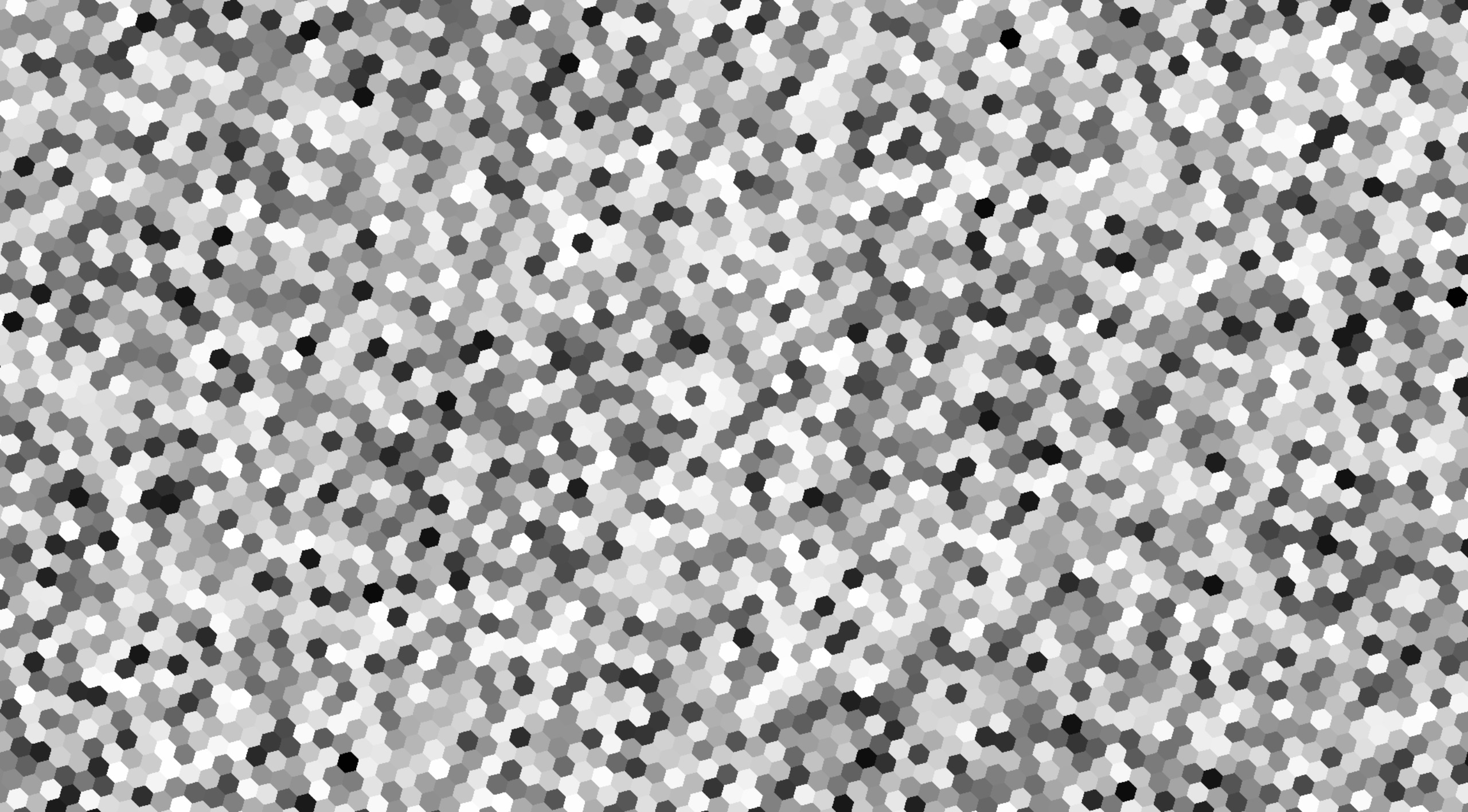
The affect is a little underwhelming with OrthoGrid since it still produces squares, but we’re not done here.
Another idea is to give each of those square corners a little nudge in some direction.
This produces a voronoi grid, which is more rigorously defined here.
For our purposes, it just makes the noise much more interesting.
Replacing SimplexGrid with Voronoi produces:

Cool! See the docs for more configuration here, like how much to nudge each point. This is the typical cellular noise. If you’ve heard of cellular noise before, this is probably what it referred to.
There’s lot’s more than just EuclideanLength, too.
Here’s a look at the shapes they produce in a distance field,
the general shape in which the distance between two points change.
EuclideanLength: produces circlesEuclideanSqrdLength: produces circles with non-linear scalingManhattanLength: produce diamondsHybridLength: combinesEuclideanLengthandManhattanLength, producing diagonal shapesChebyshevLength: produce squaresMinikowskiLength: produce concave diamonds, like stars
Here’s a look at using ManhattanLength:

Worley Noise
In cellular noise, each cell is flat since it only comes from the nearest cell point itself. So, another approach is to calculate the result based on the distances themselves rather that the point at the closest distance. This is called worley noise. Here’s how to do it in noiz:
use noiz::prelude::*;
use bevy_math::prelude::*;
let noise = Noise::<PerCellPointDistances<
Voronoi,
EuclideanLength,
WorleyLeastDistance,
>>::default();
let value: f32 = noise.sample(Vec2::new(1.5, 2.0));Here, PerCellPointDistances is told to calculate noise based on the sample location’s distance as defined by EuclideanLength to nearby points from the Voronoi partitioner,
where those distances are turned into a result via WorleyLeastDistance.
WorleyLeastDistance is a WorleyMode that does exactly what it says: returns the least distance, between 0 and 1 of course.
Here’s what that looks like:

This is traditional worley noise.
If you’ve heard of it before, this is probably what it meant.
But WorleyLeastDistance is not the only kind of worley noise.
Here’s some more, all using EuclideanLength.
WorleySmoothMin<CubicSMin>: There are other smooth min functions besides
There are other smooth min functions besides CubicSMin, but only this one is included in noiz. (But you can always make your own!) This is very similar toWorleyLeastDistance, but instead of retaining boarders between cells, this smooths those out completely, instead creating “pit” artifacts.WorleyAverage:
WorleyDifference:
WorleyRatio:
WorleyProduct:
WorleySecondLeastDistance:
One other option is to calculate the distance to the edge between the voronoi cells. This is implemented slightly differently:
use noiz::prelude::*;
use bevy_math::prelude::*;
let noise = Noise::<DistanceToEdge<Voronoi>>::default();
let value: f32 = noise.sample(Vec2::new(1.5, 2.0));It produces this: 
There’s not nearly enough space to give all length-mode combinations, but here’s one more:
 This is
This is WorleyAverage with ChebyshevLength.
Voronoi Blending
Of course, you can still blend over Voronoi.
Here’s one example:
use noiz::prelude::*;
use bevy_math::prelude::*;
let noise = Noise::<BlendCellValues<
Voronoi,
SimplecticBlend,
Random<UNorm, f32>,
>>::default();
let value: f32 = noise.sample(Vec2::new(1.5, 2.0));This makes: 
There’s also DistanceBlend<T>, where T is a length function as an alternative to SimplecticBlend.
Using DistanceBlend<ManhattanLength> for example makes:

You can also blend gradients:
use noiz::prelude::*;
use bevy_math::prelude::*;
let noise = Noise::<BlendCellGradients<
Voronoi,
SimplecticBlend,
QuickGradients,
>>::default();
let value: f32 = noise.sample(Vec2::new(1.5, 2.0));This produces:  Pretty cool!
Pretty cool!
For more information about how voronoi and worley noise works (and noise in general), check out this website.
Layered Noise
In the last two chapters, we covered all the major noise algorithms. Despite some pretty cool outputs, all the noise is still roughly the same. The noise is smooth, flowing, and organic, but it doesn’t have much variation. So, how do we add more variation? If you imagine each noise algorithm as a dice to roll, one thing you may think of is to just roll more dice! That’s the idea behind layered noise.
Interface
Layered noise is much more complex than other noise functions, so let’s take a tour of the most important types.
use noiz::prelude::*;
use bevy_math::prelude::*;
let noise = Noise::<LayeredNoise<
Normed<f32>,
Persistence,
Octave<MixCellGradients<
OrthoGrid,
Smoothstep,
QuickGradients,
>>,
>>::default();
let value: f32 = noise.sample(Vec2::new(1.5, 2.0));Here, the noise function for Noise is LayeredNoise, which is generic over a three types.
First, we need to tell it what to do with all these layers of noise.
The most common option is Normed<T>, which will add up different values of T from the layers of noise, and normalize it to the widest range of outputs of its layers, usually UNorm or SNorm.
Next, we need to tell it how to weight each layer of noise.
The most common for this is Persistence, which makes layers have progressively different contributions to the output.
By default, this will makes later noise layers “persist” exponentially less than earlier ones.
Finally, we need to actually give it the layers.
Here, we use only one layer: Octave.
An Octave is just a layer of noise that contributes directly to the output.
There are more kinds of octaves too, but we’ll cover those later.
Each Octave also needs its own generic parameter, which determines which NoiseFunction to use.
Here, we use perlin noise.
All of that is great, but the above code actually just makes standard perlin noise.
That’s because we only gave it one octave.
To add more octaves, they are listed in tuples.
For example, (Layer1, Layer2, Layer3) is itself a layer that runs Layer1, then Layer2, and then Layer3.
This is only implemented for a finite combination of tuples.
If the tuple gets too big, you’ll need to nest them, which has the same affect: (Layer1, (Layer2, Layer3)).
That lets us make this:
use noiz::prelude::*;
use bevy_math::prelude::*;
let noise = Noise::<LayeredNoise<
Normed<f32>,
Persistence,
(
Octave<MixCellGradients<
OrthoGrid,
Smoothstep,
QuickGradients,
>>,
Octave<MixCellGradients<
OrthoGrid,
Smoothstep,
QuickGradients,
>>,
Octave<MixCellGradients<
OrthoGrid,
Smoothstep,
QuickGradients,
>>,
),
>>::default();
let value: f32 = noise.sample(Vec2::new(1.5, 2.0));Tada! now we have 3 octaves of perlin noise. Here’s what that looks like:

For contrast, here’s just one layer again:

Maybe the layered one is a bit softer, has a few more details, etc, but it’s not much better. Let’s fix that!
Fractal Layers
The problem is that each layer of noise remains the same scale. This does increase the variation of the noise, but it doesn’t have a sense of “depth”. Since everything is happening at the same scale, you don’t get small details on big features–just more varied big features. Let’s fix this by making layers fractal:
use noiz::prelude::*;
use bevy_math::prelude::*;
let noise = Noise::<LayeredNoise<
Normed<f32>,
Persistence,
FractalLayers<Octave<MixCellGradients<
OrthoGrid,
Smoothstep,
QuickGradients
>>>,
>>::default();
let value: f32 = noise.sample(Vec2::new(1.5, 2.0));Here, FractalLayers repeats its inner layer some number of times (by default, 8), scaling the noise between each repetition.
When used with Normed and Persistence, this is called fractal brownian motion (fbm), and it produces this:

Very nice!
Here’s the same thing with simplex noise:

And with value noise:

Fbm noise is so common, it has a type alias in prelude::common_noise.
Configuring Noise
There’s lots of options for how to configure all the noise types we’ve covered, but it’s especially fun to do so with fbm noise.
So, how do you specify settings in Noise.
Noise<T> implements From<T>, so all you need to do is construct it from the inner NoiseFunction.
Here’s that same fbm perlin noise constructed this way:
use noiz::prelude::*;
use bevy_math::prelude::*;
let noise = Noise::from(LayeredNoise::new(
Normed::default(),
Persistence(0.5),
FractalLayers {
// The layer to do fbm with
layer: Octave::<MixCellGradients<
OrthoGrid,
Smoothstep,
QuickGradients
>>::default(),
// How much to change the scale by between each repetition of the layer
lacunarity: 2.0,
// How many repetitions to do
amount: 8,
},
));
let value: f32 = noise.sample(Vec2::new(1.5, 2.0));Note that LayeredNoise must be constructed through new, and changing it after construction is forbidden.
This is because new actually precomputes a small but meaningful portion of the work, which would be made invalid by changing the setting after the fact.
Derivatives
Up until now, we’ve mostly been concerned with the output of a noise function. But that’s not always enough. Sometime you also need to know how the noise function changes over some space. How a noise function changes is called a derivative, or more rigorously, a gradient. But since gradients can also refer to gradient noise, noiz calls them derivative in most places.
Computing Derivatives
Not all noise functions have derivatives implemented, but those that do will have a DIFFERENTIATE constant, which is off by default.
For example: MixCellGradients::<OrthoGrid, Smoothstep, QuickGradients, true> is differentiated perlin noise.
These will produce WithGradient values which contain derivative information.
These can also be collected from layered noise, ex: Normed<WithGradient<f32, Vec2>> (collect an f32 value with its gradient as a Vec2).
Specifying a gradient type also limits what kinds of input types it supports since the gradient type must match the input type.
To visualize derivatives of noise, see the “show_gradients” example:
cargo run --example show_gradients
For example, simplex noise produces these gradients:

See the red arrow? That’s the gradient of the noise at that point. The gradient always points from low values to high values (here from black to white).
Knowing the derivative of a noise function can be very useful. For example, if the noise is used as a hightmap to create landscapes, the derivative will tell you how a point on the landscape is sloping, which can be used for erosion simulations, texturing, etc. If the noise is being used for mesh generation, knowing the derivatives will allow constructing analytical normals, normals not generated strictly from geometry.
Note: All derivatives in noiz are computed analytically. This does not use a finite difference approximation. As a result, for non-differentiable functions (like absolute value), derivatives are not 100% correct everywhere. Often the gradients are “good enough” to be useful, even if they are not mathematically rigorous. Noise types do document the precision of their derivatives. If you need perfect, “as perceived” derivatives, compute a finite difference approximation instead. However, since that is rare (and very computationally expensive) it is not supported directly by noiz.
Erosion Approximation
As mentioned, derivatives can be used to simulate erosion.
But simulations are computationally expensive and require a finite landscape.
For most projects, that won’t work, but noiz supports approximating erosion too.
This works by just changing Normed to NormedByDerivative.
Let’s see an example:
use noiz::prelude::*;
use bevy_math::prelude::*;
let noise = Noise::from(LayeredNoise::new(
NormedByDerivative::<
f32,
EuclideanLength,
PeakDerivativeContribution,
>::default().with_falloff(0.3),
Persistence(0.6),
FractalLayers {
layer: Octave::<MixCellGradients<
OrthoGrid,
Smoothstep,
QuickGradients,
true,
>>::default(),
lacunarity: 1.8,
amount: 8,
},
));
let value: f32 = noise.sample(Vec2::new(1.5, 2.0));Just like Normed, we start by specifying what we want to collet, f32 here.
We could have used WithGradient<f32, Vec2> to collect the derivative of the eroded noise.
Next, we need a length function to calculate the magnitude of the gradient, here EuclideanLength, which is almost always the best option for this.
Finally, we also need to specify the erosion curve.
Here, we use PeakDerivativeContribution, which is cheap and good for making mountains.
We also use with_falloff(0.3) to configure how much affect the erosion should have.
Also, remember to turn on the DIFFERENTIATE flag.
Forgetting this is a common mistake that results in a compile error.
This produces the following: 
If you look closely, you’ll notice more natural sloping here than on ordinary perlin noise. This image is scaled up to make it easier to see, but it’s best visualized with a rendered landscape. To play around with that, run the “heightmap” example:
cargo run --example heightmap
Note that this exact example is not the landscape that is displayed, but you can make you’re own or copy the above noise function.
Faking Derivatives
Sometimes a noise function doesn’t support derivatives, but you still need it to produce them.
This may happen with NormedByDerivative, since it needs a derivative from each octave.
For those cases, noiz provides a WithGradientOf type, so you can fudge the numbers how you like.
Notably, worley noise does not support gradients, which is probably where this will be used the most.
Modifiers
Up until now, we’ve only been making, layering, and differentiating the major noise algorithms. But usually, that isn’t enough to achieve the desired artistic affect. That’s where modifiers come in.
What Are Modifiers?
There isn’t a strict definition for what modifiers are, but in general, modifiers are noise functions operate on the outputs of other noise functions rather than generating their own.
For example, noiz has a Pow4 type, which raises whatever input it is fed to the fourth power.
Modifiers like those are composed together in tuples.
For example, (PerCellPointDistances<Voronoi, EuclideanLength, WorleyLeastDistance>, Pow4) is a noise function that will first compute worley noise before raising the output to the fourth power.
Note that, like layers, this is only implemented for tuples up to a certain length.
But you can still nest them: ex: (F1, F2, F3) is the same as (F1, (F2, F3)).
Other modifiers are composed.
For example SelfMasked<PerCellPointDistances<Voronoi, EuclideanLength, WorleyLeastDistance>> will compute two different worley values and multiply them together.
Each modifier is also a noise function itself, which can be modified too. Modifiers can be composed on themselves and each other to create endless customizations!
Changing Ranges
Different noise functions produce different ranges of results.
- Gradient-based noise (
MixCellGradientsandBlendCellGradients) produce SNorm values (-1 to +1). - Distance-based noise (
PerCellPointDistancesandDistanceToEdge) produce UNorm values (0 to 1). - Value-based noise is customizable through generic parameters, ex:
Random<UNorm, f32>. - Layered noise inherits the widest range of its octaves.
But what if you want perlin noise in UNorm range instead of SNorm?
That’s easy with modifiers!
Just use (MySNormNoise, SNormToUNorm).
The inverse is also possible with the creatively named UNormToSNorm.
This is used extensively in noiz examples to display images, which need UNorm pixels.
Survey of Common Modifiers
There is no way to cover all the different modifiers and their combinations, but I’ll list some common ones.
Billowing and ping-ponging are kinda opposites of each other. Here’s fbm billowing simplex noise:
use noiz::prelude::*;
use bevy_math::prelude::*;
let noise = Noise::<LayeredNoise<
Normed<f32>,
Persistence,
FractalLayers<
Octave<(
BlendCellGradients<
SimplexGrid,
SimplecticBlend,
QuickGradients,
>,
Billow,
)>,
>,
>>::default();
let value: f32 = noise.sample(Vec2::new(1.5, 2.0));Notice how the Billow is inside of the octave.
If it were outside, it would billow the whole result, instead of each octave.
The above produce this image:

Another common operation is masking (multiplying) noise together:
Sample a noise function in the same place, but with different seeds, and multiply the results.
Here’s how to do that with SelfMasked:
use noiz::prelude::*;
use bevy_math::prelude::*;
let noise = Noise::<SelfMasked<(
LayeredNoise<
Normed<f32>,
Persistence,
FractalLayers<
Octave<
BlendCellGradients<
SimplexGrid,
SimplecticBlend,
QuickGradients,
>,
>,
>,
>,
SNormToUNorm,
)>>::default();
let value: f32 = noise.sample(Vec2::new(1.5, 2.0));Notice that this time, SelfMasked is outside the LayeredNoise.
Putting it inside is not wrong, but it produces a different affect.
Notice also that before masking, we use SNormToUNorm.
This prevents one noise function’s result from inverting the other.
Allowing that isn’t wrong either, it just makes a different result.
Anyway, here’s what this makes:

We can also mask different kinds of noise together:
use noiz::prelude::*;
use bevy_math::prelude::*;
let noise = Noise::<Masked<
MixCellGradients<OrthoGrid, Smoothstep, QuickGradients>,
BlendCellGradients<SimplexGrid, SimplecticBlend, QuickGradients>,
>>::default();
let value: f32 = noise.sample(Vec2::new(1.5, 2.0));Here, perlin and simplex noise are masked together, producing:

I wonder what worley noise masked with value noise would look like…
Raising noise to a power is also common to exaggerate its affects. Here’s what that looks like with perlin noise:
use noiz::prelude::*;
use bevy_math::prelude::*;
let noise = Noise::<(
MixCellGradients<OrthoGrid, Smoothstep, QuickGradients>,
Pow4,
)>::default();
let value: f32 = noise.sample(Vec2::new(1.5, 2.0));Which makes:

Many More
This is by no means a complete list. Check out the docs for many, many more, or modify an example to see it in action.
Warping
One of the common ways to make noise look more interesting is to use one noise function to effect the input of another. This is called domain warping.
Translation-Based Warping
The simplest way to warp noise is to run some noise function to get a vector, and add that vector to the input before passing it to another noise function.
There are two core types for this Offset, which does the adding, and RandomElements, which makes the vectors to add.
Here’s how to warp perlin noise within fbm:
use noiz::prelude::*;
use bevy_math::prelude::*;
let noise = Noise::<LayeredNoise<
Normed<f32>,
Persistence,
FractalLayers<Octave<(
Offset<RandomElements<MixCellGradients<
OrthoGrid,
Smoothstep,
QuickGradients,
>>>,
MixCellGradients<OrthoGrid, Smoothstep, QuickGradients>,
)>>,
>>::default();
let value: f32 = noise.sample(Vec2::new(1.5, 2.0));As you can see, Offset samples RandomElements to produce a vector.
That vector then offsets the input location.
The now offset input is then passed to MixCellGradients.
This produces:

Notice that the noise type for RandomElements does not need to match the one being warped, though in these examples it does.
Swapping in simplex noise in both places gives:

Notice, that the inner noise function of RandomElements can be anything that produces a scalar value.
This results in one sample per dimension, which is expensive.
Noiz provides an alternative, MixCellValuesForDomain, which is a faster version of RandomElements paired with MixCellValues.
Here’s an example of that with value noise:
use noiz::prelude::*;
use bevy_math::prelude::*;
let noise = Noise::<LayeredNoise<
Normed<f32>,
Persistence,
FractalLayers<Octave<(
Offset<MixCellValuesForDomain<OrthoGrid, Smoothstep, SNorm>>,
MixCellGradients<OrthoGrid, Smoothstep, QuickGradients>,
)>>,
>>::default();
let value: f32 = noise.sample(Vec2::new(1.5, 2.0));This produces:

Modifying-Based Warping
What if each offset applied not only to the current layer, but also to all subsequent layers?
That’s what DomainWarp does.
Here’s an example:
use noiz::prelude::*;
use bevy_math::prelude::*;
let noise = Noise::<LayeredNoise<
Normed<f32>,
Persistence,
FractalLayers<(
DomainWarp<RandomElements<MixCellGradients<
OrthoGrid,
Smoothstep,
QuickGradients,
>>>,
Octave<MixCellGradients<
OrthoGrid,
Smoothstep,
QuickGradients
>>,
)>,
>>::default();
let value: f32 = noise.sample(Vec2::new(1.5, 2.0));Notice how DomainWarp is a layer; it is not inside the Octave like Offset was.
Here’s what the above produces:

Here it is with simplex:

And with value noise:

Derivatives
When using derivatives, know that warping like this can have surprising affects. The derivatives that noiz calculates are meant to be useful and fast, not mathematically rigorous. Before assuming they are perfectly correct, test it out in the “show_gradients” example. If you see gradients that are clearly wrong, and you think they should be right or could be corrected, please open an issue in github. But in general, you should expect warped noise to have strange derivatives.
Special Partitioning
We’ve looked so far at OrthoGrid, SimplexGrid and Voronoi partitioners, but there’s actually even more options here.
Voronoi
The Voronoi graph is just a grid that has been nudged around a bit.
As has been noted, you can customize how much it nudges the grid around,
but you can also turn on a flag that approximates the graph.
This is not a perfect approximation.
It has artifacts when paired with WorleyModes that need more than just the nearest point,
and it is significantly less random than a normal Voronoi graph.
But, it is much faster.
You can enable it with a flag (off be default): Voronoi<true>.
Also, you can configure which grid Voronoi is nudging around.
It is OrthoGrid by default, but you can make your own too!
Note that
SimplexGridwill work, but not withPerCellPointDistances. This is because the domain cell it produces can’t implementWorleyDomainCell, which is needed for it to work.
OrthoGrid
OrthoGrid is actually generic over a WrappingAmount, which is the unit type (no wrapping) by default.
However, you can use OrthoGrid<i32> for example to wrap noise generated on that grid.
Vector types also work for making rectangles of wrapping noise.
You can also make your own wrapping amounts.
This is very useful if you want the result to tile.
Here’s an example of wrapping perlin noise:
use noiz::prelude::*;
use bevy_math::prelude::*;
let noise = Noise::from(
MixCellGradients {
// Wrap after 16 units.
cells: OrthoGrid(16),
gradients: QuickGradients,
curve: Smoothstep,
}
);
let value: f32 = noise.sample(Vec2::new(1.5, 2.0));The above produces:

Note that
SimplexGriddoesn’t tile in rectangles, so it is not generic over aWrappingAmount.
You can also make tiling worley noise!
use noiz::prelude::*;
use bevy_math::prelude::*;
let noise = Noise::<PerCellPointDistances<
// We need to specify that we don't want approximation,
// so we can set the custom grid to warp.
Voronoi<false, OrthoGrid<i32>>,
EuclideanLength,
WorleyLeastDistance,
>>::from(
PerCellPointDistances {
// Wrap after 16 units.
cells: Voronoi {
partitoner: OrthoGrid(16),
..default()
},
..default()
},
);
let value: f32 = noise.sample(Vec2::new(1.5, 2.0));The above produces:

More Information
This section is intended to be a reference for advanced or complex portions of the library. It exists to help answer questions that are common enough to be in the book, but not common enough to be included in the quick start.
Rng
This page covers how noiz’s rng works.
Random number generators come in lots of forms, but to make seedable, deterministic, fast noise, we need one of two options:
-
Hash functions: A hash function in this context just mashes some bits together until the result looks random enough to be visually pleasing.
-
Permutation tables: A big list of “random” values generated ahead of time by a more traditional random number generator.
Noiz uses a hash function. Permutation tables are large, take a long time to re-seed, and have a large, but finite pool of result values. A hash function’s only drawback is that they are slow in comparison.
Creating a fast enough and good enough hash function was easily the hardest part of making this library. Lots of versions still exist in the source code, commented out. Changing even a tiny part of it sometimes drastically improved some algorithms while causing major regressions in others. If there is demand, it may be possible to make the hash function generic, allowing the RNG to be customized too!
Feature Flags
Here’s all the cargo features and what they do:
Float Backend
Noiz, bevy_math, and glam all have interchangeable math backends.
The “libm” feature enables the libm math backend, which is no_std and is consistent between platforms.
The “std” feature enables the standard library’s backend, which is faster, but less consistent.
The “nostd-libm” feature will use “std” when it is available and “libm” when “std” is not available.
By default, this uses “std”.
Configuration
-
“debug”: This enables deriving
Debugfor noiz types. Noise types can get quite large and are almost never debugged, so this is disabled by default. Enable it if you need it for, well, debugging. -
“serialize”: This enables
serdefor most noise types. -
“reflect”: This derives
bevy_reflectfor most noise types.
Custom Types
If you want to make something but don’t see how to do it with only what noiz provides, you may need to make a custom noise type. This page covers some ideas for how to do that.
-
Custom modifiers: If you want to change or morph the output of a noise function(s) in a custom way, you’ll want to make a
NoiseFunction. If your modifier is math based, you can ignore the suppliedNoiseRng. If you are passing it to other noise functions, consider callingNoiseRng::re_seed, which will prevent repetition between the noise functions. -
Custom noise algorithms: If you want to make a unique algorithm, that will be a
NoiseFunction. To drive randomness, use the suppliedNoiseRngpaired with types that areNoiseRngInputs. To make that output meaningful, useAnyValueFromBitsor other functions inrng. If you are dividing floats that may be zero, see alsoforce_float_non_zero. Consider also differentiating the function analytically with calculus. Note also that many noise algorithms should be made generic over aPartitionerwhen possible. -
Custom shapes: If you want to create uniquely shaped noise, you’ll need a custom
Partitioner,DomainCell, etc. Depending on how you want it to be used, there’s a variety of traits you may wish to implement. See thecellsmodule for more information. -
Custom curves: Noiz is powered by
bevy_math, so you can use and createCurves of your own. If you want this to be usable in the context of derivatives, make sure to implementSampleDerivative. -
Custom layers: If you want to modify an input across a
LayeredNoise’s layers, you’ll need to make a custom noise layer. See thelayeringmodule for examples of this. -
Custom layer configuring: If you want more than
Normed,NormedByDerivativeandPersistence, see thelayeringmodule. Also note that depending on what you want, it may be more performant to make a separate layering system. For example, masking in noiz could be implemented as layering, but is faster throughMasked, etc. -
Custom inputs: If you want to use custom noise inputs, use
RawNoiseinstead ofNoise. You may build more abstractions from there if you wish. -
Custom outputs: If you want to do something that can’t be represented as a
NoiseFunctionand want full control, useSampleable::sample_raw, which provides access to the entropy for that sample.
Regardless of what you’re making, keep these ideas in mind:
- Be careful when working with
WithGradientvalues; remember the chain rule. - Always
#[inline]your functions. This will make theNoise-level functions very fast. The caller can decide whether to inline the final noise function or not.
Performance
This is a list of tips for writing performant noiz code. Always benchmark your noise functions. Small changes can have surprising butterfly affects!
Configuration
Make sure Cargo.toml is configured for speed.
See this guide for how to do this effectively.
Noiz is so fast because of strongly worded letters to the compiler (#[inline]) and rust’s incredible zero-cost abstractions.
Seriously, noiz is driven by traits and types and it’s just as fast as traditional megalithic functions!
Anyway, expect much worse performance when cargo has not been configured to make use of the inlining, etc.
Only Pay for What You Use
Sometimes there’s easy ways to make noise algorithms faster:
- Ensure no derivatives are being calculated but those that are needed,
- Consider turning on
Voronoi’s approximation flag, - Switch
Vec3AforVec3or visa versa, - Change “libm” backend for “std” or visa versa,
- Try
PerCellPointDistances<Voronoi, EuclideanLength, WorleyDifference>instead ofDistanceToEdge<Voronoi>, which give similar results, - Try applying
UNormToSNormand similar modifiers afterLayeredNoiseinstead of inside it, - Consider trading
RandomElementsforMixCellValuesForDomain, - Consider using
SelfMaskedinstead ofMasked, - Consider using
Linearinstead ofSmoothstep, - Consider using
WorleyNearestSmoothMininstead ofWorleySmoothMin. - Use
QuickGradientsinstead of higher quality but slower generators, - Use
RawNoiseinstead ofNoiseto skip scaling, - Use
SampleableForandsample_forinstead of their dynamic counterparts when in tight loops for better inlining,
In general, value noise is faster than perlin noise is faster than simplex noise. Sometimes it makes sense to calculate high octaves (that contribute a lot) with simplex or perlin noise, and then calculate details with value or perlin noise. For example:
use noiz::prelude::*;
use bevy_math::prelude::*;
let noise = Noise::<LayeredNoise<
Normed<f32>,
Persistence,
(
FractalLayers<Octave<MixCellGradients<
OrthoGrid,
Smoothstep,
QuickGradients,
>>>,
FractalLayers<Octave<MixCellValues<
OrthoGrid,
Smoothstep,
Random<SNorm, f32>,
>>>,
),
>>::default();
let value: f32 = noise.sample(Vec2::new(1.5, 2.0));This will generate the large features from perlin noise and use value noise to add some detail on top.
Neat Tricks
If you are filling a volume with data sourced from noise, consider sampling the noise sparsely and interpolating the results. For example, to fill an image, only sample the noise for every other pixel and fill in pixels that weren’t filled by noise based on the surrounding filled pixels. This is especially useful for voxel volume generation.
Comparing to Other Libraries
Disclaimer: I don’t maintain these other projects. There may have been updates, etc, or there may be other ways to improve their performance from a user’s perspective. If you see a way to represent them more fairly, feel free to submit a PR!
Quick Facts
| Feature | Noiz | Noise | libnoise | fastnoise_lite |
|---|---|---|---|---|
| precision | f32 | f64 | f64 | f32 |
| dimensions | 2d, 3d, 4d | 2d, 3d, 4d | 1d, 2d, 3d, 4d | 2d, 3d, |
| customizability | total | some | some | limited choices |
| cross-language | ❌ | ❌ | ❌ | ✅ |
| no-std | ✅ | ✅ | ❌ | ✅ |
| overall performance | Great | Poor | Great | Good |
| overall noise quality | Good | untested | Ok for small domains | Ok |
(If you want great noise quality, use an art application like blender.)
Benchmarks
All benchmarks are on a standard M2 Max with the same build configuration recommended above.
Each dimension’s benchmarks contain roughly the same number of samples.
All benchmarks are as even as possible. For example, they all do smoothstep interpolation, default seeding, etc.
Only a few combinations of noiz’s types are benched. If you are creating your own noise functions, it will always be best to create your own benchmarks for your own specific uses.
2D
Time (milliseconds) per 1024 ^ 2 = 1048576 samples. Lower is better.
| Noise Type | noiz | noise | libnoise | fastnoise_lite |
|---|---|---|---|---|
| value | 1.7365 ✅ | 3.1 | 1.8831 ✅ | 14.8 |
| value fbm 2 octave | 7.1 | 8.6 | 5.8 ✅ | 31.4 |
| value fbm 8 octave | 29.5 | 33.4 | 22.0 ✅ | 112.0 |
| perlin | 3.4 ✅ | 8.8 | 3.0 ✅ | 8.1 |
| perlin fbm 2 octave | 8.6 ✅ | 18.4 | 8.1 ✅ | 17.2 |
| perlin fbm 8 octave | 36.7 | 71.8 | 31.1 ✅ | 58.0 |
| simplex | 7.0 ✅ | 8.6 | 8.1 | 10.6 |
| simplex fbm 2 octave | 14.7 ✅ | 22.3 | 17.7 | 21.6 |
| simplex fbm 8 octave | 57.8 ✅ | 108.5 | 89.2 | 116.0 |
| worley | 5.7 ✅ | 24.5 | 11.8 | 17.8 |
| worley approximate | 2.8 ✅ | — | — | — |
Note that “worley approximate” is a faster version of “worley” with some compromises.
3D
Time (milliseconds) per 101 ^ 3 = 1030301 samples. Lower is better.
| Noise Type | noiz | noiz Vec3A | noise | libnoise | fastnoise_lite |
|---|---|---|---|---|---|
| value | 3.0 | 7.8 | 11.4 | 2.7 ✅ | 39.6 |
| value fbm 2 octave | 13.2 | 16.0 | 22.5 | 8.2 ✅ | 85.7 |
| value fbm 8 octave | 56.8 | 60.7 | 89.3 | 33.5 ✅ | 336.6 |
| perlin | 7.1 | 11.4 | 76.9 | 6.4 ✅ | 13.8 |
| perlin fbm 2 octave | 17.4 | 23.0 | 28.5 | 15.8 ✅ | 29.7 |
| perlin fbm 8 octave | 76.4 | 86.4 | 368.9 | 69.7 ✅ | 132.0 |
| simplex | 12.9 ✅ | 17.6 | 14.2 | 16.3 | 20.1 |
| simplex fbm 2 octave | 27.3 ✅ | 33.5 | 51.8 | 25.9 ✅ | 43.0 |
| simplex fbm 8 octave | 108.7 ✅ | 129.8 | 207.8 | 181.7 | 175.1 |
| worley | 54.8 | 57.4 | 78.9 | 52.9 | 42.3 ✅ |
| worley approximate | 6.2 ✅ | 14.9 | — | — | — |
Vec3A is an aligned 3d type from bevy_math (glam). It enables SIMD instructions, but uses more memory to do so.
As you can see, it’s not worth it here.
4D
Time (milliseconds) per 32 ^ 4 = 1048576 samples. Lower is better.
| Noise Type | noiz | noise | libnoise | fastnoise_lite |
|---|---|---|---|---|
| value | 13.8 | 21.2 | 3.9 ✅ | — |
| value fbm 2 octave | 27.7 | 46.0 | 14.3 ✅ | — |
| value fbm 8 octave | 109.0 | 167.3 | 57.3 ✅ | — |
| perlin | 17.5 ✅ | 177.6 | 17.6 ✅ | — |
| perlin fbm 2 octave | 38.3 ✅ | 53.5 | 38.4 ✅ | — |
| perlin fbm 8 octave | 146.1 ✅ | 824.2 | 203.1 | — |
| simplex | 18.8 ✅ | 35.5 | 29.5 | — |
| simplex fbm 2 octave | 36.6 ✅ | 108.8 | 41.0 | — |
| simplex fbm 8 octave | 139.3 ✅ | 421.0 | 234.4 | — |
| worley | 186.8 | 156.3 ✅ | 205.8 | — |
| worley approximate | 26.3 ✅ | — | — | — |
Summary
For value noise, libnoise is the clear winner for performance.
Both fastnoise_lite and noise are far behind. noiz is close, but not quite as fast.
This is because libnoise uses a permutation table for it’s rng where noiz uses a custom hash function.
This mean two things:
First, libnoise will invalidate a cache line, which is not reflected in these benches since nothing was competing for the cache.
Second, libnoise will produce repeating noise from far away.

See the tiling? This is at a frequency of 200.
By contrast, here’s noiz at a frequency of 1024:

No tiling. Yay! Note that some artifacting (not quite tiling) does happen at excessively large scales. But that’s not a big deal in practice. (Ever wonder why the far lands exist in minecraft?)
For perlin noise, noiz and libnoise roughly tie for 2d; noiz is faster for 4d but libnoise just beats it for 3d.
This is likely also due to the difference in rng methods, and the same quality issues and benchmark blind spots apply here too.
For simplex noise, noiz is the clear winner. Simplex is about half as fast as perlin for 2d, but it gets better for higher dimensions, beating perlin in 4d.
For Worley noise, the results vary greatly depending on use-case. See for yourself.
What to Choose
Use fastnoise_lite if you need consistncy across languages.
Use libnoise if you don’t need a ton of configuration, are using relatively small domains, and are primarily doing value and perlin noise.
If you absolutely need f64 support, use libnoise, but again, the permutation table rng makes the large domain kinda a moot point. Same goes for noise.
If you are integrating with bevy, need lots of customization, need general, high performance, or need serialization and reflection, use noiz.
I am not aware of a reason to use noise (though there may well be one I’m missing).
Learning Resources
This is a list of places that teach how noise actually works mathematically. This background can be helpful for debugging any artifacting, etc, that may appear.
- This website covers lots of cool math and some noise implementations.
- This video visually explains value and perlin noise.
- This paper explains simplex noise.
This list is not at all exhaustive but hopefully provides enough context to get you started if you’re curious.
Changelogs
This section covers how noiz has changed between versions.
V 0.2
This is a small release, mostly focusing on rounding some rough edges from 0.1. If there are any issues you run across, please don’t hesitate to open an issue!
Enhancements
When collecting results of layered noise, Normed and NormedByDerivative can now collect gradients. Ex: Normed<WithGradient<f32, Vec2>>.
This is the proper way to collect gradient information of fractal layered noise and is very useful for things like analytical normals for mesh generation.
A new noise function, WithGradientOf, can now be used to “fudge” a gradient value.
Although this will not be correct, it can be artistically useful when paired with NormedByDerivative, or other systems that use gradient information to affect the output.
A new Lerped curve now allows interpolating between vector space values.
This is particularly helpful when combined with the new RemapCurve noise function.
A noise function, Translated, has been added to replace the Offset<Constant> pattern.
The prelude::common_noise module has been expanded to include derivatives of common noise.
In general, I prefer to use the noise types directly, rather than these aliases; that opens up more customization and demystifies the actual algorithm.
However, in some places, shorter names are preferred, and now derivatives are possible there too.
Bug Fixes
It’s hard to define a “bug” when it comes to noise, since there’s no real correct vs incorrect for most systems; just whether or not it “feels” random enough in the right ways. That said, there were a few bug-like fixes over 0.1.
Some gradients were not mathematically rigorous; they were often “good enough”, but they weren’t correct.
Many of these are now fixed, including simplex noise, fractal noise, masked noise, and linearly mapped noise (like UNormToSNorm).
Notably, Abs, Billow, and NormedByDerivative are still not mathematically rigorous.
These do not appear to be classically differentiable, but “good enough” implementations are still provided.
Perlin noise is now normalized to ±1; it was ±(1/√N) where N was the number of dimensions. This was previously not normalized for performance (it’s a linear scale, which the user will configure anyway), but it has been fixed to help with usability. With fast-math coming in rust 1.88, this will be made zero cost in the future.
Migration Guide
Blender and DiferentiableGradientBlender have been replaced by ValueBlender, DifferentiableValueBlender, GradientBlender, and DifferentiableGradientBlender.
The functionality of these traits remains the same, but this separation allows more specific implementations.
The LayerOperationFor trait has been expanded over the new LayerResultContextFor.
This will not affect most users, but if you were making custom layers, this will need to be migrated.
Scaled now scales directly rather than going through a nested noise function.
If you want the previous behavior, use Masked.
I have deliberately kept this brief, as these changes are unlikely to affect anyone, but if you have any trouble migrating, please open an issue!
What’s next
It’s hard to predict the future here, as I have limited time, and lots of my ideas here depend on other projects. However, there are some things I’d like to explore for the future:
- 64 bit support: Noiz is powered by bevy_math, which is growing to support 64 bit precision.
When that work is complete, Noiz will upgrade to support
f64based inputs and outputs. - even faster: Rust 1.88 brings support for fast-math, offering some insane performance opportunities at the cost of precision. This will probably be an opt-out feature, as it is not without downsides, but this is still up for debate.
- Other rng backends: Noiz is powered by a very specialized and optimized random number generator. Some power users may want to make their own generators to either sacrifice quality for speed or speed for quality.
- GPU support: This is especially tricky to think about. Some forms of noise don’t even make sense on the GPU (but lots do!). As projects like WESL and rust GPU make more progress, I’d like to explore getting noiz on the GPU. This is still a long way off but is something I’m looking into.
- Reflection noise types: As bevy editor prototypes and progress continues, making the noise types more customizable and changeable at runtime is important. Adding more reflection support will help with this. Designing this features is difficult without compromising speed, so don’t expect this too soon, but know that it is in the works!
If you have any other requests, please open an issue or PR! Feedback is always welcome as I work to make this the “go to” noise library for bevy and rust.
Release 0.3
Enhancements
Added PowI and Sqrt math noise functions.
Upgraded to Bevy 0.17.
Bug Fixes
Fixed some places where float operations did not use the proper backend. This is unlikely to have affected anyone but is fixed now.
Fixed voronoi graphs not reporting correct values for worley noise. This was causing noise values to not be properly normalized for some values of voronoi randomness. Fixing this decreased the average brightness/value of some worley modes. If you would prefer to increase the value to match the behavior in 0.2, the noise can still be scaled afterwards.
Migration Guide
In theory, if it compiled for 0.2, 0.3 should also compile (aside from any Bevy-related changes). If you run into any trouble migrating, please let me know.
What’s next
It’s hard to predict the future here, as I have limited time, and lots of my ideas here depend on other projects. However, there are some things I’d like to explore for the future:
- 64 bit support: Noiz is powered by bevy_math, which is growing to support 64 bit precision.
When that work is complete, Noiz will upgrade to support
f64based inputs and outputs. Currently, this is blocked by Bevy’sCurvetrait. - even faster: Rust 1.88 brought support for fast-math, offering some insane performance opportunities at the cost of precision.
However, this feature is not completely stable and definitely has downsides. Plus,
glamwould need to add support for it first. - Other rng backends: Noiz is powered by a very specialized and optimized random number generator. Some power users may want to make their own generators to either sacrifice quality for speed or speed for quality.
- GPU support: This is especially tricky to think about. Some forms of noise don’t even make sense on the GPU (but lots do!). As projects like WESL and rust GPU make more progress, I’d like to explore getting Noiz on the GPU. I have spent some time looking at options for implementations, and I do not see this happening any time soon, unfortunately.
- Reflection noise types: As bevy editor prototypes and progress continues, making the noise types more customizable and changeable at runtime is important. Adding more reflection support will help with this. I have looked at this a lot, even with the help of some users, and I also don’t see this coming any time soon. But we’ll see.
If you have any other requests, please open an issue or PR! Feedback is always welcome as I work to make this the “go to” noise library for bevy and rust.
Limited development
Please note that while all of these features are on my list, most of them are blocked externally. I am also working on a number of other very exciting projects, so Noiz is (for now) being more maintained than developed.
Noiz is fast because everything is monomorphized and inlined at compile time. However, on some platforms, rust does not fully use SIMD. There is room for another noise library to support fully dynamic noise with manually implemented SIMD optimizations. Such a library would likely out perform Noiz for large blocks of samples but under perform for specific samples or samples that can not be placed on a grid. This is one of the projects I’d like to work on, and there are many more.
Release 0.4
This release is just an upgrade from bevy 0.17 to 0.18. If you run into any issues upgrading, please open an issue.
Improving Noiz
Noiz is open source. If you feel something is missing, please open an issue or pull request.
There’s still lots more that can be added here:
- GPU support,
- Custom RNGs,
- Reflection based noise types
- (and more)
At the same time, I don’t want to volunteer my time for features nobody needs. So please make issues for any feature requests you may have etc.
With any luck, we can make Noiz the number one noise library for rust!